摘要: 春风入画寻芳迹,数学藏趣探幽径清明时节,草长莺飞,正是踏青寻春、追思怀古的好时节。你是否曾在祭扫时留意过墓碑排列的几何规律?在漫步公园时好奇过如何用一条路线走遍所有桥却不重复?当 “清明踏青” 遇上 “ ...
春风入画寻芳迹,数学藏趣探幽径
清明时节,草长莺飞,正是踏青寻春、追思怀古的好时节。你是否曾在祭扫时留意过墓碑排列的几何规律?在漫步公园时好奇过如何用一条路线走遍所有桥却不重复?当 “清明踏青” 遇上 “数学探秘”,一场跨越时空的思维之旅就此展开 —— 2025年4月2日漯河五高趣味数学社团的指导老师马锐莉带领社员,从欧拉路径的视角,重新发现春日里的 “图论密码”。

(数学家欧拉)一、清明・七桥之问:当传统邂逅数学1. 哥尼斯堡的春日谜题18 世纪的哥尼斯堡(今俄罗斯加里宁格勒),普雷格尔河穿城而过,河上有七座桥连接两岸与小岛。当地居民曾热衷于一个问题:能否一次性走完七座桥,且每座桥只走一次?这个看似简单的 “踏青路线规划” 问题,最终由数学家欧拉在 1736 年破解,成为图论的起点 ——欧拉路径(一笔画问题)由此诞生。
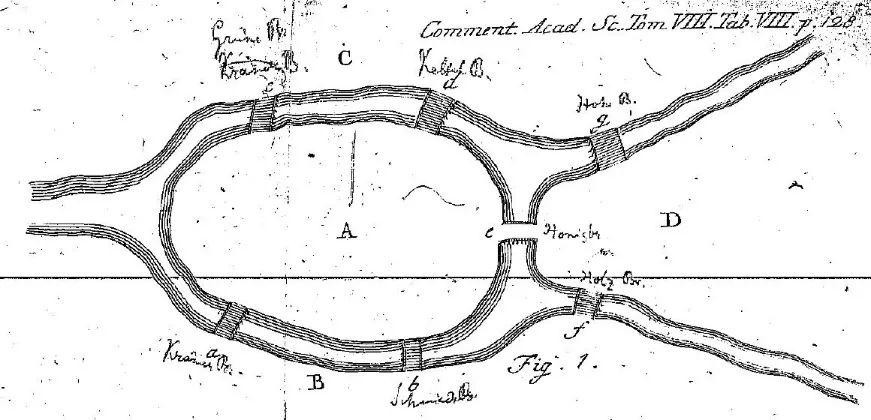
欧拉将陆地抽象为 “顶点”,桥梁抽象为 “边”,问题转化为:在 “图” 中是否存在一条路径,经过每条边一次且仅一次?他发现了关键规律: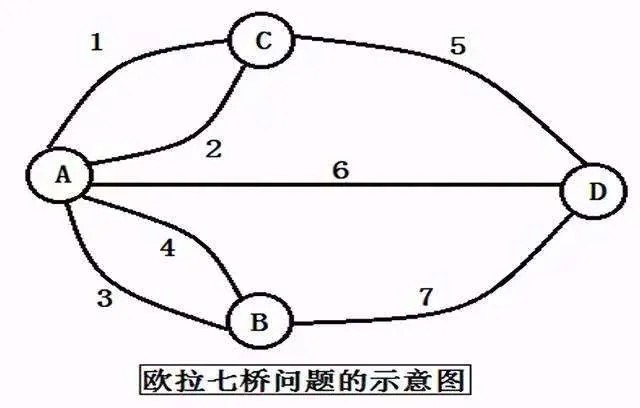
·欧拉路径:若图中恰好有 0 个或 2 个度数为奇数的顶点,则存在这样的路径(0 个奇数顶点时为回路,即起点终点相同)。·度数:顶点连接的边数,比如三岔路口的度数为 3(奇数),十字路口度数为 4(偶数)。二、清明寻迹:生活中的欧拉路径实践1. 祭祖路线:不走回头路的智慧清明扫墓时,若家族墓碑分布在多个区域,如何设计一条不重复的路线,高效祭拜?画个 “祭祖图”:将每个墓碑区视为顶点,连接道路为边,计算各顶点度数。若有 2 个奇数顶点:从其中一个起点,终点为另一个奇数顶点,即可 “一笔走完”;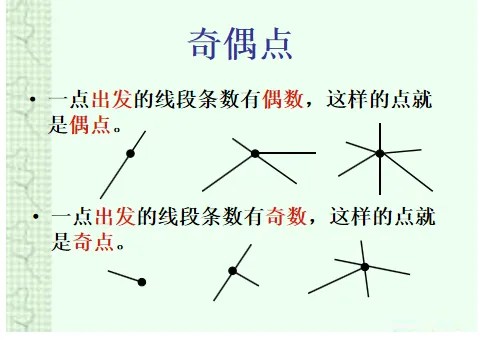
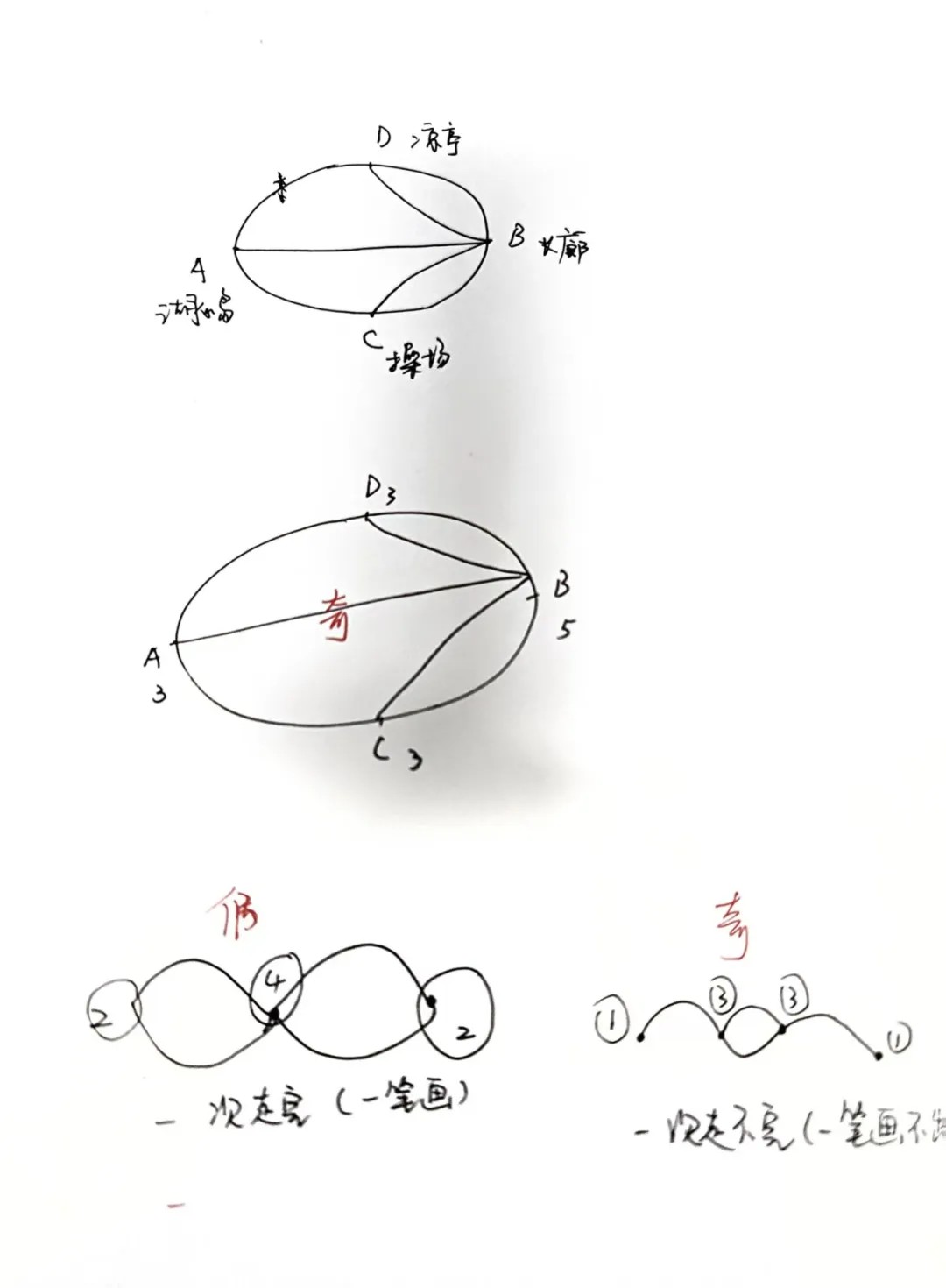
以绘制校园的 “清明路线图”,标注顶点度数,湖心岛、凉亭、长廊、操场构成顶点,桥梁和步道为边。同学们实地测绘后发现:若某条步道正在维修(去掉一条边),图中奇数顶点数变为 2,即可规划一条 “不走回头路” 的踏青路线;若所有顶点度数均为偶数,不妨从任一景点出发,最终回到起点,完成 “完美环游记”。
三、当清明遇见欧拉:数学的浪漫从未缺席从千年传统的清明踏青,到三百年前的数学突破,人类对 “路径” 的探索从未停止。欧拉路径不仅是图论的基石,更教会我们:用数学的眼光观察世界,平凡的风景也能绽放智慧的光芒。正如清明既是追思过往的节点,也是迈向新生的起点,数学思维让我们在 “连接” 与 “遍历” 中,找到秩序与美感的平衡。春日寄语下次踏青时,不妨带着 “欧拉的眼睛”:数一数路口的 “度数”,画一张简易的 “路线图”;试试用 “一笔画” 走完所有想逛的景点,让数学成为踏青的最佳向导!愿这个清明,我们在追思中感悟传统,在探索中遇见数学的诗意 |





















